牛顿为了得到正弦函数sinX的无穷级数，他首先用几何方法快速的得出了反正弦函数arcsinX的无穷级数形式，这在上一篇文章已经讨论过了首先假设sinZ=X图一上一篇中我们已经得到图二因为sinZ=X，

牛顿为了得到正弦函数sinX的无穷级数，他首先用几何方法快速的得出了反正弦函数arcsinX的无穷级数形式，这在上一篇文章已经讨论过了

首先假设sinZ=X

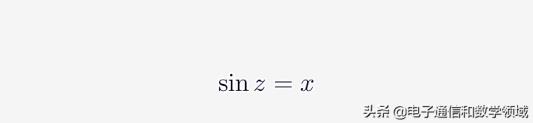
图一

上一篇中我们已经得到

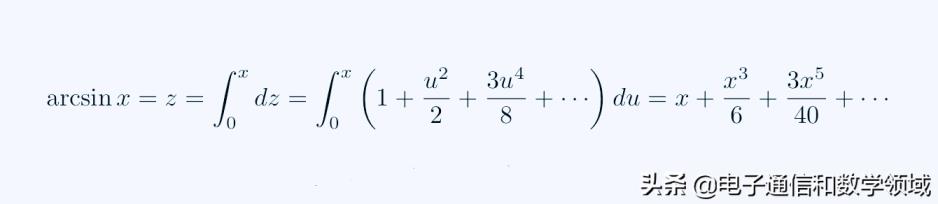
图二

因为sinZ=X，所以Z等于

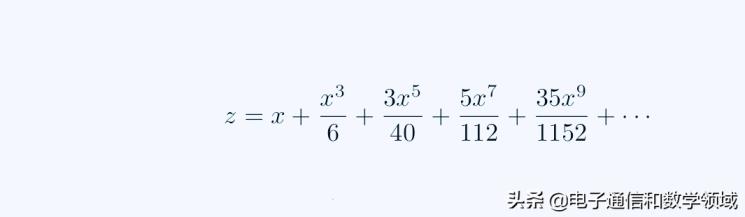
图三

牛顿由此将上式写成一个等式方程的形式，如下图所示，

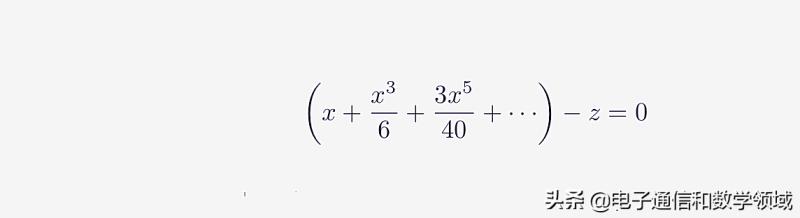
图四

牛顿的锦囊妙计就是，他不直接去求X表示的弧长Z的级数，而是寻思相反的过程。牛顿利用他的逆过程，将Z=arcsinX级数转换成X=sinZ的级数。

首先牛顿舍弃所有指数大于2的项，这样就得到X-Z=0 从而逆级数X=Z

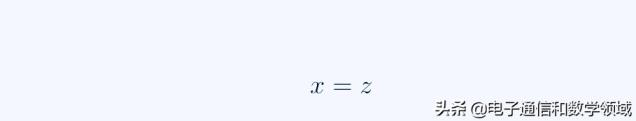
图五

牛顿认识到舍弃全部高阶项会导致不准确的结果，准确的答案应该具备X=Z+P，其中P是待定的级数，如下图

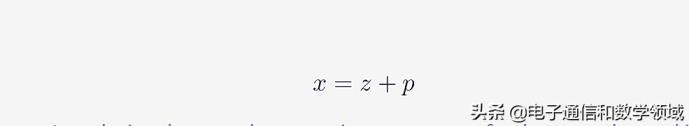
图六

将X=Z+P带入arcsinX的级数中得到

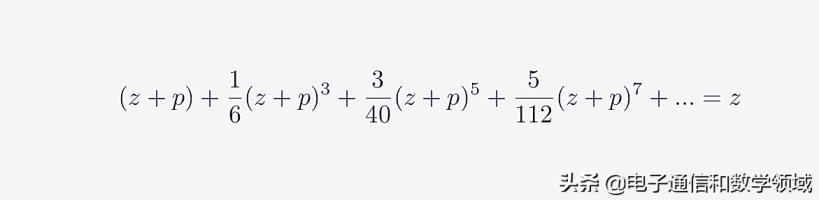
图七

全部展开整理得到如下结果

图八

牛顿在这里舍弃上述方程中P的2次方，3次方和更高次方项，求解得到

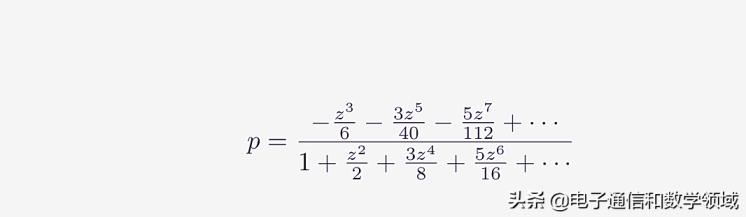
图九

牛顿进行第二轮删除，他舍弃分子中除Z最低次方外的所有高次方项，舍弃分母中的所有Z的高次方，就得到P=-Z^3/6+q,，这里的q是仍是一个待确定的级数，

此时我们就得到sinZ级数的前两项Z-Z^3/6

图十

为了确定q，我们将其带入 图七，得到

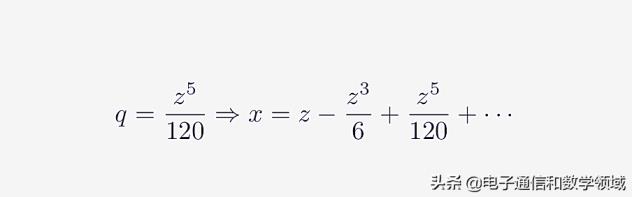
图十一

同样可以求出q的值等于Z^5/120，所以我们得到了sinZ级数的前三项

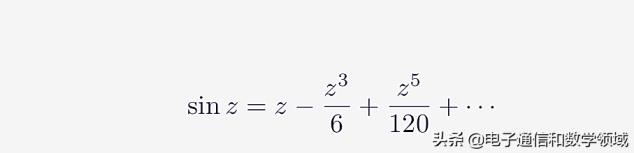
图十二

依次类推，牛顿就推导出了正弦函数sinZ的无穷级数的所有项

牛顿推导sinX的原过程